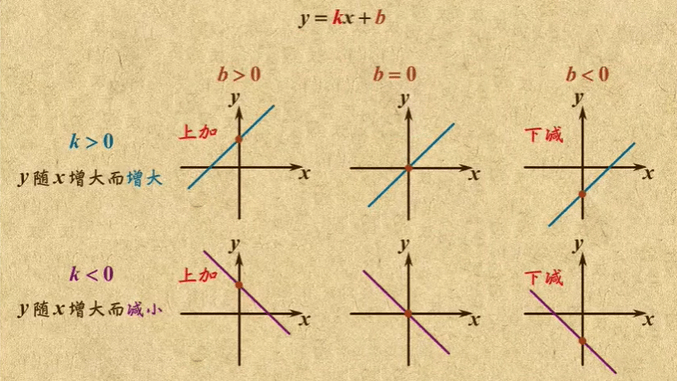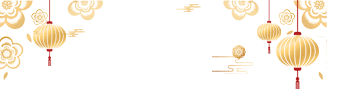解析用一次函数来实现瞄准线的反射，绘制实线加虚线方法(未完)

摘要

今天想到KUOKUO大佬很早以前分享的“用一次函数来实现瞄准线的反射”的文章链接直达http://www.kuokuo666.com/kk023.html,

并下载了大佬的Demo进行学习，由于数学基础一般在阅读大佬代码时有很多不理解在此进行解析分析，以便以后学习，感谢各位

大佬们的开源精神；

瞄准线分三种：无效果直射、遇墙反射、遇墙与球体反射。今天进行解析了第二种：遇墙反射。

版本说明

使用 CocosCreator 的 2.4.3 版本演示。

一次函数

一次函数是什么：一次函数是函数中的一种，一般形如y=kx+b（k，b是常数，k≠0），其中x是自变量，y是因变量。特别地，当b=0时，y=kx（k为常数，k≠0），y叫做x的正比例函数（direct proportion function）

公式：y=kx+b （注意：k、b是常数，并且k≠0）

变化：k = y/x -b；

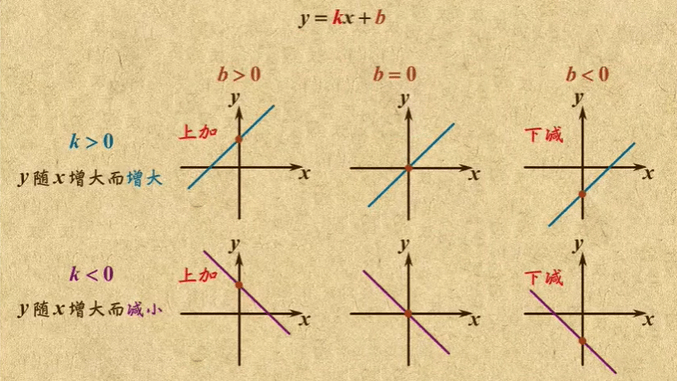
你是不是又在疑惑什么是自变量、因变量、常数，下面就给你简单讲解下，了解的朋友请忽略。

假如你去买苹果，苹果4元一斤

• 买一斤为4元
• 买两斤为8元
• 买x斤为y元 即 y = 4x

那么在这个式子中 4 为常量，而你买多少斤苹果的x就为自变量，买苹果花费是钱y这是因变量，他是根据你买的斤数x进行变化

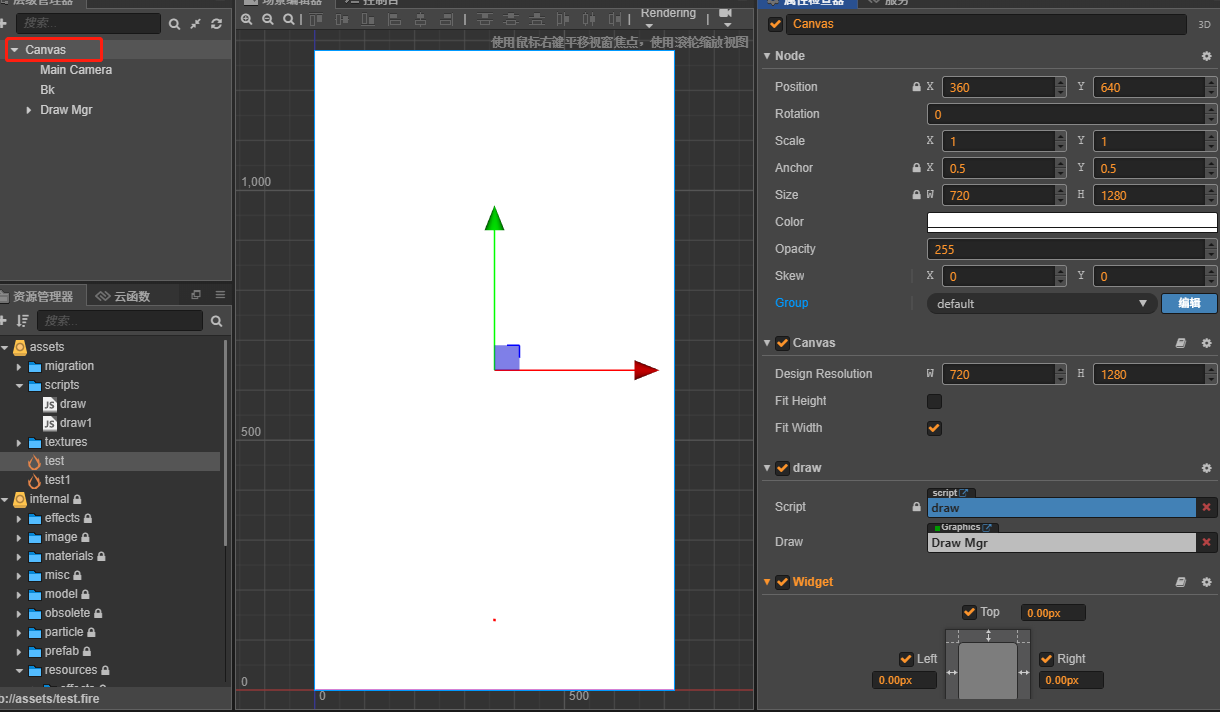
界面搭建脚本挂载

脚本挂载在Canvas上并且在Draw Mgr节点上添加Graphics组件，脚本上定义Graphics组件属性。

全部代码

let POS = cc.Enum({
    LEFT: -360,
    RIGHT: 360,
    WIDTH: 720,
});
cc.Class({
    extends: cc.Component,

    properties: {
        draw: cc.Graphics,
    },

    start () {
        this.node.on(cc.Node.EventType.TOUCH_START, (e) => {
            // cocos中自带的触摸事件都是返回世界坐标 世界想用需要局部需要进行转换
            let pos = this.draw.node.convertToNodeSpaceAR(e.getLocation());
            this.drawLine(pos);
        }, this);

        this.node.on(cc.Node.EventType.TOUCH_MOVE, (e) => {
            let pos = this.draw.node.convertToNodeSpaceAR(e.getLocation());
            this.drawLine(pos);
        }, this);

        this.node.on(cc.Node.EventType.TOUCH_END, (e) => {
            this.clearLine();
        }, this);
    },
    
    drawLine (pos) {
        // 清空上次绘制
        this.draw.clear();
        // 求出k是为了 判断k是否大于0 区分是向右还是向左 以及斜率
        // 已知x y 求k 即 k = y / x; 为什么没有-b因为初始坐标点是(0,0)所以b=0
        let k = pos.y / pos.x;
        // 线的长度 即瞄准线的长度
        let lineLength = 1200;
        // 设置绘制起点，在Draw Mgr节点下的cc.ve2(0,0)并不是Draw Mgr节点位置
        this.draw.moveTo(0,0);
        // 默认起点位置，用于下方求长度
        let point = cc.v2(0, 0);
        // 定义常数b，b从原点出发所以等于0
        let b = 0;
        // 定义x，y位置
        let x, y;
        // 算一下 b 的增长值 即为反射的线
        let d_b = (k > 0 ? POS.RIGHT : POS.LEFT) * k;
        // 起始标志
        let isRebound = false;

        while (true) {
            // 根据K判断当前墙的x点
            x = k > 0 ? POS.RIGHT : POS.LEFT;
            // 一元函数 y = k·x + b
            y = k * x + b;
            // 到达墙壁所需长度 
            let l = cc.v2(x, y).sub(point).mag();
            // 如果到达墙线的长度小于剩余长度 说明反射线正常
            if ( lineLength > l) {
                isRebound = true;
                // 扣去已经过长度
                lineLength -= l;
                // 添加一个新点 然后在画布中创建从该点到最后指定点的线条
                // 绘制实线
                // this.draw.lineTo(x, y);
                // 绘制虚线
                this.dottedDrawLine(point,cc.v2(x, y))
                // 更改下一轮循环起始点
                point.x = x;
                point.y = y;
                // 获取b的长度 y+增量
                b = y + d_b;
                // 斜率取反
                k *= -1;
            } else {
                // 如果不能到墙，分为两种情况，需要一个标志
                // 表示削减后
                if (isRebound) {
                    // 剩余长度 除以 到达墙壁所需要的长度
                    let l_k = lineLength / l;
                    // 
                    let r_x = POS.WIDTH * l_k;
                    x = k > 0 ? POS.LEFT + r_x : POS.RIGHT - r_x;
                    y = k * x + b;
                } else {
                    let l_k = lineLength / l;
                    let r_x = POS.WIDTH / 2 * l_k;
                    x = k > 0 ? r_x : -r_x;
                    y = k * x;
                    // 中心处理
                    if (x > -0.05 && x < 0.05);
                    y = lineLength;
                }
                // 绘制实线
               // this.draw.lineTo(x, y);
               // 绘制虚线
               this.dottedDrawLine(point,cc.v2(x, y))
                break;
            }
        }
        // 绘制实线时打开
        // this.draw.stroke();
    },
    clearLine () {
        this.draw.clear();
    },

    dottedDrawLine (start,end) {
        // 获得组件 
        let com = this.draw 
        // 获得从start到end的向量 
        let line = end.sub(start) 
        // 获得这个向量的长度 
        let lineLength = line.mag()
        // 设置虚线中每条线段的长度 
        let length = 20 
        // 根据每条线段的长度获得一个增量向量 
        let increment = line.normalize().mul(length) 
        // 确定现在是画线还是留空的bool 
        let drawingLine = true
        // 临时变量 
        let pos = start.clone() 
        // com.strokeColor=cc.color(255,255,255) 
        // 只要线段长度还大于每条线段的长度 
        for(;lineLength > length; lineLength -= length) { //画线 
           if(drawingLine) { 
                   com.moveTo(pos.x,pos.y)
                   pos.addSelf(increment)
                   com.lineTo(pos.x,pos.y) 
                   com.stroke() 
               } else { 
                   pos.addSelf(increment)
                } 
                // 取反 
                drawingLine=!drawingLine 
        } 
       // 最后一段 
        if(drawingLine) { 
             com.moveTo(pos.x,pos.y) 
             com.lineTo(end.x,end.y) 
             com.stroke() 
          } 
       },
});

效果展示

难点标注

1. 一次函数 y = k * x + b
2. 反射线增量即b的位置
3. 最后反射线位置
4. 向量运算，sub() 、mag()、normalize()、mul()、clone()